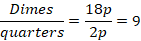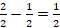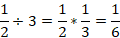Which of the following is the total number of whole boxes that measure 4 ft * 4 ft * 4 ft that can be stored in a room that measures 11.5 ft * 11.5 ft * 11.5 ft, if the size of the boxes cannot be altered?
A. 10
B. 24
C. 20
D. 18
The number of boxes is determined by volume of the room divided by volume of one box.
Number of boxes
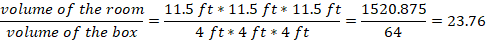
Therefore, about 24 boxes can be stacked in the room.
Therefore, the Correct Answer is B.
More Questions on TEAS 7 Math
-
Q #1: A child has collected 100 pennies, 90 nickels, 50 dimes, and 5 quarters. Which of the following charts accurately organizes the number of coins? Chart 1 Chart 2 Chart 3 Chart 4
A. Chart 1
B. Chart 2
C. Chart 3
D. Chart 4
Answer Explanation
C organizes the collection correctly.
-
Q #2: A child has a bottle full of pennies, nickels, dimes, and quarters. There are twice as many quarters as pennies, three times as many as nickels as pennies, and six times as many dimes as nickels. How many more dimes does the child have than quarters?
A. 10 times as many
B. 5 times as many
C. 6 times as many
D. 9 times as many
Answer Explanation
In this task, we use the relation from the given scenario to compare the number of dimes to quarters.
If we let p be number of pennies in the bottle. Then,
Number of quarters in the bottle = 2p
Number of nickels in the bottle = 3p
Number of dimes in the bottle =6(3p)=18p
Now relating dimes to quarters, we have
Thus, there are 9 times as many dimes as quarters in the box.
-
Q #3: Five friends are sharing a pizza. Two friend eats half of the pizza. The other three friends equally divide the rest among themselves. What portion of the pizza did each of the other three friends receive?
A. 1/6
B. 1/3
C. 5/6
D. 1/5
Answer Explanation
we need to find the portion of pizza shared by other three friends.
Two friends eat half of the pizza, which is ½
And the remaining amount of pizza,
Now, the other three friends share ½ amongst themselves equally. Then, each friend gets
The other three friends each gets 1/6 of the pizza.
