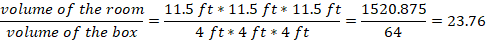Which of the following is the equivalence in pounds for 65 kg? (2.2 lb=1 kg)
A. 52.2 lb
B. 22.7 lb
C. 143 lb
D. 220 lb
To find the pounds equivalent of the kg given, we use the two options as given below.
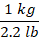
OR
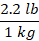
Since we want to remain with pounds, we use the second option and set up the equation below.
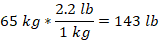
Thus, 65 kg is equal to 143 lb.
Therefore, the Correct Answer is C.
More Questions on TEAS 7 Math
-
Q #1: Which of the following is the total number of whole boxes that measure 4 ft * 4 ft * 4 ft that can be stored in a room that measures 11.5 ft * 11.5 ft * 11.5 ft, if the size of the boxes cannot be altered?
A. 10
B. 24
C. 20
D. 18
Answer Explanation
The number of boxes is determined by volume of the room divided by volume of one box.
Number of boxes
Therefore, about 24 boxes can be stacked in the room.
-
Q #2: An energy company’s stock price was $65.50 on Monday. On Tuesday, the price went up $1.50. On Wednesday, the price decreased from Tuesday’s price by $2.57. On Thursday, the price went up $2.25 from Wednesday’s price. Which of the following was the final price on Thursday?
A. $66.68
B. $65.79
C. $67.00
D. $64.43
Answer Explanation
We are tasked to find the stock price on Thursday from the given information. Here, we need to find the stock of each day from the price increase or decrease. If the price increases, we add to the previous day’s price and subtract if the price decreases.
Monday’s stock price=$65.50
Tuesday’s stock price is Monday’s plus $1.50=65.50+1.50=$67.00
Wednesday’s stock price went down by $2.57 from Tuesday’s=67.00-2.57=$64.43
Thursday’s stock price went up by $2.25 from Wednesday’s =64.43+2.25=$66.68
From the above evaluation, the stock price on Thursday was $66.68
-
Q #3: Solve for A in the equation below. Diagram:
A. A = t(kr+P)
B. A = (kr+P)/t
C. A = P-kr/t
D. A = kr-t/P
Answer Explanation
P-At=-kr
Subtract P on both sides
P-P-At=-kr-P
-At=-kr-P
Divide both sides by -t
-At/-t=(-kr-P)/-t
A=(kr+P)/t
