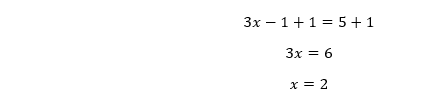To determine the cost of a meal, the restaurant considers the quantity of the meal, the number of toppings, and the types of spices. Which of the following is the dependent variable?
A. Size of meal
B. Cost of meals
C. Type of spices
D. Number of toppings
A dependent variable changes with any change made in an independent variable. From this case, cost of meals depends on other three options. In other words, the quantity of meal, number of toppings, and types of spices influence the cost of the meal.
Therefore, the Correct Answer is B.

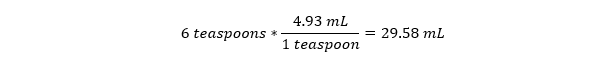
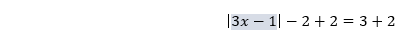

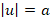 , a>0, then u=a or u=-a
, a>0, then u=a or u=-a