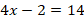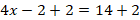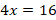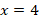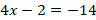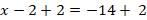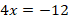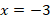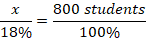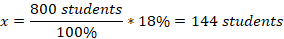The American with Disabilities Act (ADA) requires that the slope of a wheelchair ramp be no greater than 1:12. Which of the following is the minimum length of a ramp needed to provide access to a door that is 1.5 feet above the sidewalk?

A. 22 feet

B. 19.5 feet

C. 32.5 feet

D. 18 feet

Answer Explanation:

The slope represents the ratio of rise to run. Let p be the minimum length of the ramp, we can set a ratio equation as follows. Then,

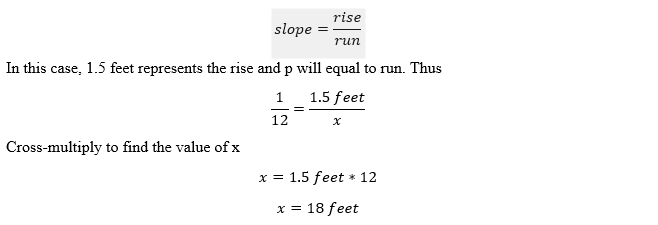
The minimum length of the ramp needed is 18 feet to access to a door that is 1.5 feet above the sidewalk.

Therefore, the Correct Answer is D.

Q #1: Which of the following is the value of x in the equation below

A. x= -3 or x=4

B. x= -1 or x=2

C. x =-2 or x= 4

D. x= -3 or x= 5

Answer Explanation

We are tasked to find the unknown values of x in the given equation.

First, we add 8 to both sides of the equation.

Next, we apply the absolute rule:

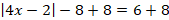
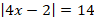
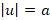If , a>0, then u=a or u=-a

From our resulting equation, a=14, which is greater 0. Then, the first condition (u=a) becomes

Solving for x

The second condition (u= -a) becomes

Solving for x

Thus, the value of x is 4 or -3
Q #2: Which of the following is the mean of the test scores listed below? 99, 93, 67, 48, 92, 87

A. 67

B. 48

C. 99

D. 81

Answer Explanation

the mean of a data set is the sum of the scores divided by the number of tests.

Total test scores =99+93+67+ 48+ 92+ 87=486

Number of tests =6

Mean test score =486/6=81

The mean test score is 81.
Q #3: There are 800 students enrolled in four allied health program at a local community college. The percent students in each program is displayed in the pie chart. Which of the following is the number of students enrolled in the dental hygiene program?

A. 168

B. 144

C. 336

D. 152

Answer Explanation

we are to use the pie chart to find the number of students enrolled in dental hygiene care.

Letting x represent the number of students enrolled in dental hygiene care, we set the proportion equation with number of students as numerator and percentage as denominator. It should be noted that the whole pie chart represents 100% of the 800 students. Then,

We solve the value of x by cross-products.

Therefore, 144 students will enroll for a dental hygiene program.