The American with Disabilities Act (ADA) requires that the slope of a wheelchair ramp be no greater than 1:12. Which of the following is the minimum length of a ramp needed to provide access to a door that is 5.2 feet above the sidewalk?
A. 52 feet
B. 148 feet
C. 32.2 feet
D. 62.4 feet
In this problem slope represents the change in height above sidewalk to change in length of the ramp.
From the definition of slope
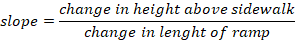
Letting x to be the minimum length of the ramp, then
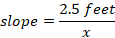
Substituting with the known value of slope
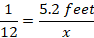
Cross-multiply to find the value of x
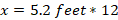
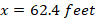
Thus, the minimum length of the ramp needed is 62.4 feet to access to a door that is 5.2 feet above the sidewalk.
Therefore, the Correct Answer is D.
More Questions on TEAS 7 Math
-
Q #1: A child has a bottle full of pennies, nickels, dimes, and quarters. There are four as many quarters as pennies, three times as many as nickels as pennies, and five times as many dimes as nickels. How many more dimes does the child have than pennies?
A. 5 times as many
B. 10 times as many
C. 20 times as many
D. 15 times as many
Answer Explanation
Explanation:
In this question, we need to find the ratio of dimes to quarters.
If we let x be number of pennies in the bottle. Then,
Number of quarters in the bottle = 4x
Number of nickels in the bottle = 3x
Number of dimes in the bottle =5(3x)=15x
Now relating dimes to quarters, we have
Thus, there are 15 times as many dimes as pennies in the box.
-
Q #2: A motor company’s stock price was $33.20 on Tuesday. On Wednesday, the price went up $2.45. On Thursday, the price decreased from Wednesday’s price by $1.50. On Friday, the price went up $1.62 from Thursday’s price. Which of the following was the final price on Friday?
A. $35.65
B. $34.15
C. $35.77
D. $34.82
Answer Explanation
-
Q #3: A child has a bottle full of pennies, nickels, dimes, and quarters. There are three as many quarters as pennies, five times as many as nickels as pennies, and two times as many dimes as nickels. How many more dimes does the child have than nickels?
A. 4 times as many
B. 5 times as many
C. 2 times as many
D. 10 times as many
Answer Explanation
In this question, we need to find the ratio of dimes to quarters.
If we let x be number of pennies in the bottle. Then,
Number of quarters in the bottle = 3x
Number of nickels in the bottle = 5x
Number of dimes in the bottle =2(5x)=10x
Now relating dimes to quarters, we have
Thus, there are 2 times as many dimes as nickels in the box.
