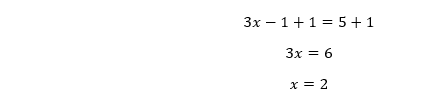The American with Disabilities Act (ADA) requires that the slope of a wheelchair ramp be no greater than 1:12. Which of the following is the minimum length of a ramp needed to provide access to a door that is 5.0 feet above the sidewalk?
A. 60 feet
B. 145 feet
C. 32.5 feet
D. 30 feet
To find the minimum length requires, we need to understand what slope in the question represents. The slope represents the ratio between the height to the length. Let x be the minimum length of the ramp. Then,
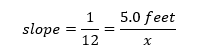
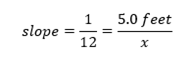
Now, we find the value of x by cross-products as follows
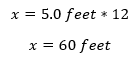
Thus, the minimum length required to provide access is 60 feet.
Therefore, the Correct Answer is A.
More Questions on TEAS 7 Math
-
Q #1: A child has a bottle full of pennies, nickels, dimes, and quarters. There are six as many quarters as pennies, two times as many as nickels as pennies, and 5 times as many dimes as nickels. How many more dimes does the child have than nickels?
A. 4 times as many
B. 5 times as many
C. 20 times as many
D. 10 times as many
Answer Explanation
In this problem, we need to compare the number of dimes to quarters.
If we let p be number of pennies in the bottle. Then,
Number of quarters in the bottle = 6p
Number of nickels in the bottle = 2p
Number of dimes in the bottle =5(2p)=10p
Now relating dimes to nickels, we have
Thus, there are 5 times as many dimes as quarters in the box.
-
Q #2: Simplify the expression below. Which of the following is correct? \(\frac{[3 (2 + 6 \ast 4)]}{(26 \div 2)}\)
A. 6
B. 8
C. 12
D. 9
Answer Explanation
We follow the order of operations to solve the given expression.
First, we start with the numerator and solve it as follows
[3(2+6*4)]
We start with multiplication in inner brackets, 6*4=24. The expression becomes
[3(2+24)]
Then, we conduct the addition of 2+24=26. Then, the expression becomes
[3(26)]=3*26=78
Now, we solve for denominator, which is 26/2=13.
Thus, the expression is reduced into
\(\frac{[3(2+6\ast4)]}{(26\div2)}=\frac{78}{13}=6\)
The expression reduces into 6.
-
Q #3: Which of the following is the value of x in the equation below
A. x= -4/3 or x=2
B. x= -1 or x=2
C. x =-2 or x= 1
D. x= -3/2 or x= 1/2
Answer Explanation
we find the value of x by applying the absolute conditions to the given equation.
First, add 2 to both sides of equation
Add 10 to both sides of the equation
Next, we apply the absolute rule:
If u=a
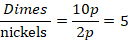
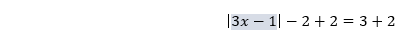
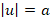, a>0, then u=a or u=-aIn this case a=5, which is greater 0.
The first condition becomes
Solving for x
The second condition becomes
Solving for x
Then, the value of x is -4/3 or 2.
