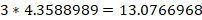How many milliliters are there in 6.5 liters?
A. 0.65
B. 65
C. 650
D. 6500
We use the relation 1 L=1000 mL to convert L to mL.
The two options for converting between L and mL are
And
We use the first option to convert 6.5 L to mL as follows:
Thus, 6.5 L is 6500 mL.
Therefore, the Correct Answer is D.
More Questions on TEAS 7 Math
-
Q #1: A person weighed themselves at 153 lb. Five months later they weighed themselves at 120 lb. Which of the following is the percent of weight the person lost over 5 months? (Round to the nearest percent.)
A. 38%
B. 22%
C. 19%
D. 29%
Answer Explanation
The percentage change in weight is found in three steps below:
Absolute change in weight=final weight-initial weight
Absolute change in weight= (left|120-153 ight|=left|-33 ight|=33)
Relative change in weight= (frac{absolute change}{initial weight}=frac{33}{153}=0.216)
Percent change=relative change * 100%
Percent change=0.216*100%=21.6%
The percent change in weight lost is 21.6 %, which is about 22%.
-
Q #2: Which of the following is the best approximation of 3 times the positive square root of 19?
A. 57
B. 13.1
C. 21.7
D. 6.9
Answer Explanation
We use the calculator to find the positive square root of 19, which is then multiplied by 3.
Using the calculator,
Multiplying the square root above with 3 becomes
The approximate value of 3 times the square root of 19 is 13.1.
-
Q #3: A bucket containing 2 2/5 gallons of water is 4/7 full. How many gallons of water is in one fully filled bucket?
A. 4 1/5
B. 2 1/5
C. 4 4/5
D. 2 2/5
Answer Explanation
we are asked to find the number of gallons a full tank can hold. A full tank is equivalent to 1.
Convert the mixed fraction into proper fraction as follows
(2frac{2}{5}=frac{left(2ast5 ight)+2}{5}=frac{10+2}{5}=frac{12}{5})
If we let x be the number of gallons in full tank, and setting up the proportion equation with the number of gallons on the numerator and fraction of tank on denominator as follows.
(frac{x gallons}{1 full tank}=frac{frac{12}{5} gallons}{frac{4}{7}full tank})
Cross-multiply to find the value of x.
(frac{x }{1 full tank}=frac{frac{12}{5} gallons}{frac{4}{7}full tank})
(x astfrac{4}{7}full tank=frac{12}{5} gallonsast1 full tank)
(x =frac{frac{12}{5} gallonsast1 full tank}{frac{4}{7}full tank}=frac{12}{5}divfrac{4}{7} gallons=frac{12}{5}astfrac{7}{4}gallons=frac{21}{5}gallons)
Converting 21/5 to a mixed fraction is 4 1/5. Thus, when the tank is full, it holds 4 1/5 gallons of water.
