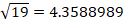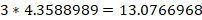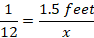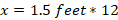A recipe calls for 3 teaspoons of vanilla. 1 teaspoon equals approximately 4.93 mL. Which of the following is the correct amount of vanilla in mL?
A. 34.33 mL
B. 9.58 mL
C. 10.49 mL
D. 14.79 mL
To find the amount of vanilla in mL, use dimensional analysis of the units of measurements.
Two ways to convert between teaspoon and mL are:
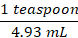
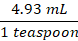
Since we are required to find the amount in mL, we use a cionverstioon that will result in mL. Inspecting the above options, we use the second option and set up an equation in way the unwanted units cancel out and leave the wanted unit we are looking for. Then,
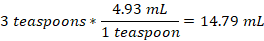
Thus, a recipe of 3 teaspoons equals 14.79 mL.
Therefore, the Correct Answer is D.
More Questions on TEAS 7 Math
-
Q #1: Which of the following is an appropriate unit of measure to express the length of a chair?
A. Centimeters
B. Kilometers
C. Micrometers
D. Milligrams
Answer Explanation
The length of the chair could be appropriately measured in centimeters. Kilometers are used to measure long distances while micrometers could be used to measure the length of small microorganism in microbiology lab. However, milligrams are used to measure the masses of small quantities.
-
Q #2: Which of the following is the total number of whole boxes that measure 4 ft * 4 ft * 4 ft that can be stored in a room that measures 11.5 ft * 11.5 ft * 11.5 ft, if the size of the boxes cannot be altered?
A. 10
B. 24
C. 20
D. 18
Answer Explanation
The number of boxes is determined by volume of the room divided by volume of one box.
Number of boxes
Therefore, about 24 boxes can be stacked in the room.
-
Q #3: How many milliliters are there in 6.5 liters?
A. 0.65
B. 65
C. 650
D. 6500
Answer Explanation
We use the relation 1 L=1000 mL to convert L to mL.
The two options for converting between L and mL are
And
We use the first option to convert 6.5 L to mL as follows:
Thus, 6.5 L is 6500 mL.
