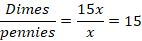A person weighed themselves at 120 lb. Three months later they weighed themselves at 160 lb. Which of the following is the percent of weight the person gained over 3 months? (Round to the nearest percent.)
A. 66%
B. 33%
C. 35%
D. 30%
We need to find the percent change in weight of a person. To find the percent change, follow the following steps:
- Find absolute change in weight
- Find relative change
- Find the percent change from relative change.
Absolute change is the difference between the final value and initial value. Our initial value is 120 lb and final value is 160 lb. Then,
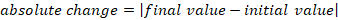
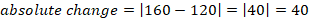
Relative change is given by
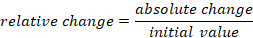
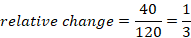
Percent change is determined by
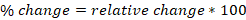
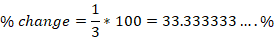
To the nearest whole number, the percent change is 33%.
Therefore, the Correct Answer is B.
More Questions on TEAS 7 Math
-
Q #1: A cheese recipe calls for 1/2 cup of flour for every 3/8 cup of milk. To make a bigger batch, the chef uses 3 cups of flour. Which of the following would be the amount of milk needed for the bigger batch?
A. 2 ¼ cups
B. 1 3/4 cups
C. 4 cups
D. 2 ¾ cups
Answer Explanation
-
Q #2: A recipe calls for 6.5 teaspoons of vanilla. 1 teaspoon equals approximately 4.93 mL. Which of the following is the correct amount of vanilla in mL? (Use the conversion rates as provided)
A. 32.05 mL
B. 29.55 mL
C. 34.20 mL
D. 25.80 mL
Answer Explanation
Explanation:
We need to find the mL in 6.5 teaspoons from the given information.
If we let x represent the amount of vanilla in mL, and set a proportion equation with number of teaspoons as numerator and mL as denominator, then:
(frac{6.5}{x} = frac{1}{4.93})
Find the value of x by cross-products
6.5 * 4.93 = x
32.05 = x
Therefore, 6.5 teaspoons equal 32.05 mL.
-
Q #3: A person weighed themselves at 190 lb. Three months later they weighed themselves at 180 lb. Which of the following is the percent of weight the person lost over 3 months? (Round to the nearest percent.)
A. 8%
B. 9%
C. 11%
D. 5%
Answer Explanation
Explanation: The percentage change in weight is found in three steps below:
Absolute change in weight = final weight - initial weightAbsolute change in weight = (|180 - 190| = |-10| = 10)
Relative change in weight = (frac{absolute change}{initial weight} = frac{10}{190} = 0.0526)
Percent change = relative change * 100%
Percent change = 0.0526 * 100% = 5.26%
The percent change in weight lost is 5.26%, which is about 5%.
