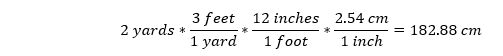A child has a bottle full of pennies, nickels, dimes, and quarters. There are six as many quarters as pennies, two times as many as nickels as pennies, and 5 times as many dimes as nickels. How many more dimes does the child have than nickels?
A. 4 times as many
B. 5 times as many
C. 20 times as many
D. 10 times as many
In this problem, we need to compare the number of dimes to quarters.
If we let p be number of pennies in the bottle. Then,
Number of quarters in the bottle = 6p
Number of nickels in the bottle = 2p
Number of dimes in the bottle =5(2p)=10p
Now relating dimes to nickels, we have
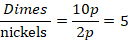
Thus, there are 5 times as many dimes as quarters in the box.
Therefore, the Correct Answer is B.
More Questions on TEAS 7 Math
-
Q #1: Which of the following is the best estimate of the number of centimeters (cm) in 2 yards? (Note: 1 yard=3 feet; 1 foot =12 inches; 1 inch =2.54 cm)
A. 175 cm
B. 180 cm
C. 136 cm
D. 90 cm
Answer Explanation
we convert the given value in yards to the cm by setting up the equation below.
2 yards is equal to 182.88 cm, which is approximately 180 cm.
-
Q #2: -2/9, -0.9, -1.7, -4/7 Of the number listed above, which number is the greatest?
A. -0.9
B. -4/7
C. -1.7
D. -2/9
Answer Explanation
The initial step is to convert the decimal options to fractions. Then, we find the LCM of the denominators of all fractions, which will be used to compare the values of the given options.
-0. becomes -9/10
-1.7 becomes -17/10
Then, the resulting denominators are 9, 10, and 63. Their LCM of 630 is used to multiply each fraction.
-2/9*630=-140
-9/10*630=-567
-17/10*630=-1071
-4/7*630=-360
From the calculations above, -140 is the greatest value of all the values. Thus, -2/9 is the greatest number.
-
Q #3: The length of a rectangular room is 8 feet greater than its width. Which of the following equations represents the area (A) of the room?
A. A = w(w+8)
B. A = 2w+2(w+8)
C. A = 5(w+8)
D. A = w+(w+8)
Answer Explanation
To find the area of the room, we form an equation of find an equation relating the length and width of the rectangle. If we let the width of the room to be w, then
Width of the rectangle= w
Length of rectangle=(w+8)
Area of the rectangle, A= Length*width=(w+8)*w
A=w(w+8)
Thus, the area of the rectangular room is w(w+8).
