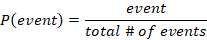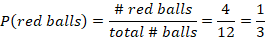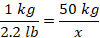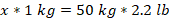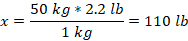A bucket containing 2 4/5 gallons of water is 1/3 full. How many gallons of water is in one fully filled bucket?
A. 14/15
B. 2 7/15
C. 8 2/5
D. 6 4/5
We are asked to find the number of gallons full tank can hold. The fraction of full tank is 1.
First, we let x be the number of gallons in full tank. Then, set the proportion equation by setting the number of gallons on the numerator and fraction of tank on denominator as follows.
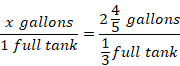
Convert the mixed fraction into proper fraction and cross-multiply to find the value of x.
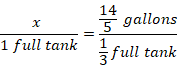
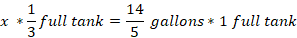
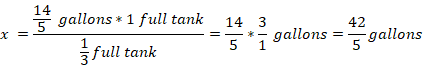
Converting 42/5 to a mixed fraction is 8 2/5. Thus, when the tank is full, it holds 8 2/5 gallons of water.
Therefore, the Correct Answer is C.
More Questions on TEAS 7 Math
-
Q #1: A bag contains five green balls, four red balls, and three yellow balls. If one ball is randomly selected from the ball, which of the following is the probability that the ball is red?
A. 5/12
B. ¼
C. ½
D. 1/3
Answer Explanation
The probability of an event is determined by the relation
Finding the probability of drawing the red ball, we need to find the total number of balls in the bag.
Total number of balls in the bag=5+4+3=12 balls
The probability of drawing a red ball from the bag is 1/3.
-
Q #2: Which of the following is the equivalence in pounds for 50 kg? (2.2 lb=1 kg)
A. 52.2 lb
B. 22.7 lb
C. 110 lb
D. 220 lb
Answer Explanation
We are asked to convert kg to pounds using the given relation. Letting x to represent the lb we are looking for.
Nest, we set the proportion with kg in the numerator and lb on the denominator as follows.
We find the value of x by cross-multiplication
The value of x is 110 lb.
-
Q #3: Which of the following is the median of the date set below? 5, -3, 10, -2, 0
A. 5
B. 2
C. 10
D. 0
Answer Explanation
To find the median, we arrange the following numbers in data set from the smallest to the largest as follows.
-3, -2, 0, 5, 10
From the above the data set, the median falls in the third position. Thus, 0 is the median for the given data set.
