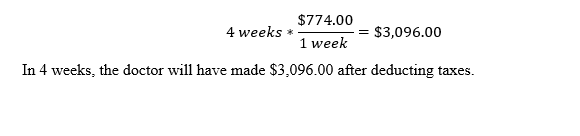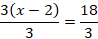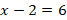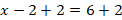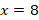A bucket can hold 5000 mL. How many L can the bucket hold?

A. 500L

B. 5L

C. 50L

D. 0.05L

Answer Explanation:

To change between L and mL, the following two options are used.

Therefore, the Correct Answer is B.

Q #1: A doctor earns $980.00 per week before any tax deductions. The following taxes are deducted each week: $85.00 federal income tax, $40.00 state income tax, and $81.00 Social Security tax. How much will the doctor make in 4 weeks after taxes are deducted?

A. $3,096.00

B. $3,00.00

C. $3,00.00

D. $3,200.00

Answer Explanation

We are required to find the doctor’s earning in 4 weeks after taking off taxes.

The first step is to find the total weekly deductions as follows:

Total weekly tax=federal income tax + state income tax + Social Security tax

Total weekly tax=$(85.00+40.00+81.00)

Total tax=$206.00

The next step is to find the weekly income after deducting total taxes

Weekly net income=gross income-total tax

Weekly net income=$(980.00-206.00)=$774.00

In one week, the net income of the doctor is $774.00 and after 4 weeks, the net income will be 4 times his weekly earning
Q #2: Twelve less than thrice a number Which of the following translates the phrase above into a mathematical expression?

A. 3x - 12

B. 12 - 3x

C. 12x - 2

D. 3x + 12

Answer Explanation

We need to form a mathematical expression from the given word problem.

Let the unknown number be x.

Thrice a number is three times = 3x

Twelve less than thrice a number = 3x-12

Thus, the mathematical expression from the word problem is 3x-12
Q #3: 3 (x-2) = 18 Solve the equation above for x. Which of the following is the correct answer?

A. 8

B. -5

C. 7

D. 4

Answer Explanation

We solve for the value of x by following the order of operations

3(x-2)=15

Divide both sides of the equation by 3

Add 2 to both sides of the equation

Thus, the value of x is 8.